5 Serial Dilution - matespdfs40’s blog

Serial Dilution Introduction: The Purpose of serial dilution is to determine the number of bacteria per unit volume in the origi-nal culture, determination of the.

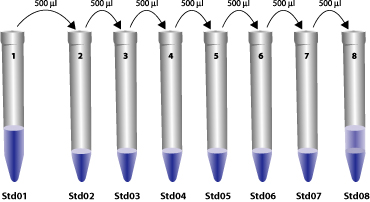
Serial Dilution

The dilution factor. When you re thinking about dilution, it helps to simplify your actions into dilution factors. When we said the diluted coffee was.

Dec 25, 2013 Serial Dilution Method: Definition and Procedure Explained.

Serial dilution

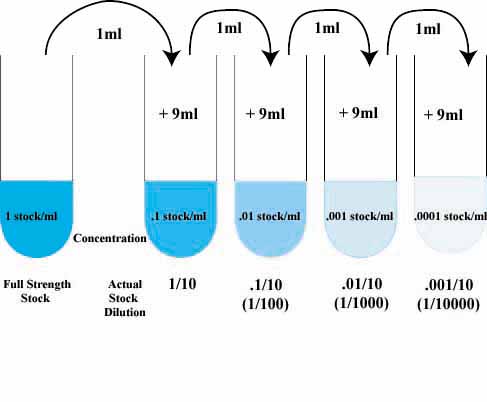
Dilution calculation with simple c1v1 c2v2 dilution equation. Just enter concentrations and volume to get V1 for your stock solution.

The story on the previous pages has many parallels with life in a microbiology lab. Frequently, you will find it necessary to add water or some other medium to a stock or soup, get it. with a known concentration to make a more dilute solution.

Why would you want to do this. Let s say you need to get 1/10,000th of a mL in order to count the bacteria in it. That would be pretty difficult with a pipette. But instead, you could

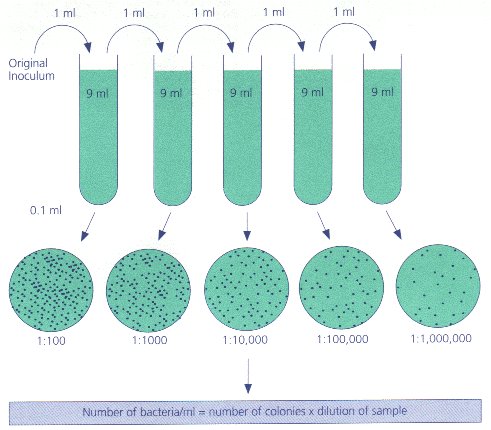
Take that 1 mL and put it in 99 mLs of saline solution. You still have the same number of bacteria, but now they re spread out.

Now you can take 1 mL of THAT solution, add it to a new container, top off with 99mLs of water, and you ll have only 1/100th of the original bacteria in the mL.

Pull out 1 mL of this latest mixture, and you ll have 1/100th of 1/100th, which is multiplying the fractions together 1/10,000th.

When you do serial dilutions, you multiply together all of the dilution factors. Make sure you are clear on what constitutes a dilution factor. When I add a small amount of the concentrated stuff to an empty container, top it off with saline/water/whatever, then remove some small amount, this constitutes a dilution. So above, even though its broken down into 3 steps, there are really only 2 full dilution steps.

When in doubt, try to think it through logically. Often it helps to think through the whole process using some concrete number. For example: I started with 300,000 cells in a mL, put those into 99 mLs of saline, and took out a mL, so there must have been 3,000 cells in that mL. Then I put those 3,000 cells into 99 mLs of saline, and took out one mL again, so there must have been 30 cells in that mL. Overall my dilution must have been to 30 from 300,000, which is the same as to 1 from 10,000 ,000. Of course, the idea that you started with 300,000 cells is pure fiction, but it can help you make sure that you ve done the dilutions correctly.

Put one mL of a stock into 99 mLs of water. Take 1 mL of that and put it in 999 mLs of water. What is the total dilution.

To make this problem interactive, turn on javascript.

I need a hint :Assume that you start with 1,000,000 cells in one mL of solution

another hint :After first dilution, you are left with 10,000 cels in one mL of solution

another hint :After second dilution, you are left with 10 cells in one mL of solution

another hint :Multiply two dilution factors to get the total dilution

I think I have the answer: 0,000

Start with a 00 dilution someone else has made. Take 1 mL and put it in 99 mLs of water. What is the total dilution.

I need a hint :Assume that you start with 10,000 cells in one mL of solution

another hint :After first dilution, you are left with 100 cells in one mL of solution

another hint :First dilution factor is 0

another hint :Multiply the dilution factor you obtained with the initial dilution factor to get the total dilution

Put one mL of a stock into 49 mLs of water. Take 1 mL of that and put it in 49 mLs of water. What is the total dilution.

I need a hint :Assume that you are starting with 20,000 cells in one mL of solution

another hint :After first dilution you are left with 400 cells in one mL of solution 20,000/50

another hint :After second dilution you are left with 8 cells in one mL of solution 400/50

another hint :Multiply two dilution factors 1/50 1/50 to get the total dilution

I think I have the answer: 00

Put one mL of a stock into 99 mLs of water. Repeat 3 more times. What is the total dilution.

I need a hint :Assume you are starting with 1,000,000,000 cells in one mL of solution

another hint :After first dilution you are left with 10,000,000 cells in one mL of solution dilution factor 0

another hint :Dilution factor is the same each time

another hint :Multiply all four dilution factors to get total dilution

I think I have the answer: 0,000,000

Start with a ,000 dilution someone else has made. In order to get a 0,000 dilution, you need to put 1 mL into __ mLs of water.

I need a hint :Determine the dilution factor to get 0,000 dilution from ,000 dilution

another hint :Dilution factor is

another hint :You need to have 10 mL of solution to get 0,000 of dilution

I think I have the answer: 9

Starting with a dilution made by a TA, you add 1 mL to 49 mLs of water to get a 0,000 dilution. What was the TA s dilution factor.

I need a hint :Your dilution factor is

another hint :Divide final dilution with your dilution factor to get initial dilution

I think I have the answer: ,000

If we put dilution and scaling up together, we can estimate the number of bacteria in the original sample. For example:

If a ,000 dilution results in a plate with 176 CFUs, then the original number of bacteria in the sample.

I need a hint : Remember you have basically counted 1/10,000th of the original bacteria.

another hint : Multiply by the reciprocal of the dilution factor

one more hint : Don t forget that we re only reporting 2 significant digits.

I think I have the answer: approximately 1,800,000.

Pretty easy, right. The only tricky part is that you don t know in advance how far to dilute your original sample. Let s see what happens if you always count a ,000 diluted sample. If your original solution contained

50,000,000 bacteria: the ,000 sample will contain about 5,000 CFUs. You would be counting all day and the CFUs overlap and it s a mess.

500,000 bacteria: the diluted sample will contain about 50 CFUs, which is both easy to count and valid for scaling up.

50,000 bacteria: the diluted sample will contain ON AVERAGE 5 CFUs. But remember that diluting and sampling is bascially a random process, and imagine the havoc caused by one extra CFU ending up in your pipette -- suddenly you estimate the population as 60,000 rather than 50,000, and you re off by 20.

5000 bacteria: the diluted sample will contain ON AVERAGE 0.5 CFUs -- meaning that any given sample will probably contain either 0 or 1 CFU. This will be easy to count, but its not valid for scaling up.

So here s the general rule: in order to be valid, the plate that you scale up should contain between 25 and 250 CFUs. Any more than 250 CFUs can cause overlap, and you ll underestimate the population size. Any fewer than 25 makes your estimate vulnerable to over- OR under-estimates based on random chance alone.

So the real trick here is picking the correct dilution. For the 50 million bacteria case, 1:1,000,000 would have been a good dilution facter. For the 5 thousand bacteria case, 0 would have done the trick. And since you can t know ahead of time what that is, instead you ll need a series of dilutions.

A series of dilutions ensures that one of these dilutions will be in the countable range 25 to 250 CFUs.

So let s put this all together. We would like to count the bacteria in a particular sample, and we think that there should be in the neighborhood of 10 million cells per mL.

Ideally, therefore, we would like to get 100 bacteria on the plate that we count. That would be a dilution factor of 1,000,000, or 0,000. And to give ourselves a little wiggle room, we should start at least 1 dilution before that, so ,000. Then we ll do three more dilutions to get our series.

In the table below, click on the button corresponding to the plate that should be used to estimate the original concentration of bacteria:

dilution factor

,000

0,000

1:1,000,000

,000,000

count

475

answer

Pretty straightforward, right. Below, you can practice a couple more times. I also included a few unusual situations things do go wrong, of course, and you should be able to recognize that. If you think the dilution series is not valid, click on re-do the dilution.

dilution factor

0,000

1:1,000,000

,000,000

0,000,000

count

TNTC

674

answer

375

105

,000

249

954

567

Before you head off, I just want to say a few words about resolution.

Even if you have perfect technique in mixing and pipetting, you cannot determine the exact number of bacteria present in your sample. This is an unavoidable consequence of diluting and scaling up.

Let s imagine that we have a sample with exactly 183,000 cells per mL. And let s say that our technique is flawless. If we count a ,000 diluted plate, we should find 183 CFUs remember, we have magically flawless technique. But the exact same thing would happen if our sample started with 183,001 cells. Or 183,100 cells. Or 183,400 cells. Or 182,800 cells. In fact, even with our absolutely flawless technique, the best we can say is that there are between 182,500 and 183,500 cells. So our absolutely unavoidable error is plus or minus 500/182,000 -- about 0.27. That s pretty good.

Let s look at some other ways we could count the same 183,000 cell sample:

Dilution Factor

plate count

resolution

ease of counting

1830

/- 50

0.027

NOPE, can t do it

183

/- 500

0.27

boring but do-able

/- 5000

2.7

easy

/- 50,000

chimpanzees can do this

So you can see that the 25 to 250 guideline is really a compromise between the ability to distinguish non-overlapping CFUs, and the resolution afforded by the scaling up component.

In the applet below, you can practice the whole process of serial dilution from beginning to end. If you don t get a good count the first time, try it again.

Hint: this applet previews the module on bacterial growth rates a bit. Specifically, you need to know that the doubling time is the amount of time it takes a population to double. So if you start with a population of 100 and it doubles every 10 minutes, after a half hour it has doubled 3 times to about 800.

Scaling up is technique used to estimate the size of huge population of bacteria based on the calculations from smaller sample.

Serial dilution is a step by step dilution of concentrated solution into diluted solution, where each dilution gets you closer to your goal.

You can multiply together all of the dilution factors to get total dilution factor.

It is very important to dilute sample up to a certain extent, so that the number of cells/bacteria are in countable range. If after a dilution, the number of cells/bacteria is between 25 and 250, they are both easy to count and valid for scaling up.

It is also important to know that even if you have perfect technique in mixing and pipetting, you can only estimate the number of bacteria present in your sample. It is impossible to know the exact number of bacteria.

If you want a printer-friendly version of this module, you can find it here in a Microsoft Word document. This printer-friendly version should be used only to review, as it does not contain any of the interactive material, and only a skeletal version of problems solved in the module.

MathBench Measurement

Serial Dilution:

Counting Small Round Things

This module is currently under revision

In this module, we re going to consider some practical implications of counting bacteria. Primarily, we re going to deal with 2 questions:

how do I count something that runs into the millions or billions.

what are the pitfalls.

We ll talk about a specific method serial dilution, plating, counting, and scaling up, but I want to make it clear at the outset that the problem of counting huge numbers of things is not at all unique to counting bacteria. Many of the same issues scaling up, error propagation apply to other things that people want to count, like insects, birds, contaminants, pollutants, human population

So, we re going to start by talking about scaling up.

Richard Feynman, one of the most celebrated physicists in modern times, was famous for beginning his first-year honors physics class at Caltech by asking the students to estimate how many barbers work in Chicago. Presumably he was not interested in getting a haircut. Instead, he was in part asking his students to scale up an estimate based on small sample.

So, for example, you might estimate that in one square urban mile there is on average one barber shop just barbers, not hairdressers with 2 barbers. And the area of Chicago is about 2100 square miles according to Wikipedia. So,

if there are 2 barbers per square mile, and

2100 square miles in Chicago

then how many barbers are there in Chicago.

The answer of course is 2100 2 approximately 4200. And in fact you would be approximately right. According to one website, there are 4140 barbers in Chicago in early 2006 -- and according to that same website, this is a question sometimes used in job interviews to determine how well candidates think on their feet. Talk about far-reaching applications of mathematical concepts.

So let s try a few more:

How many plastic shopping bags are used per year in the U.S..

Clearly this is not something you want to go out and count. But without doing a few calculations, its impossible to make even an informed guess. Is it billions. trillions. more.

Instead, try making an informed guess, based on your own use of plastic bags, and a US population of 300 million people

I need a hint : How many bags do you use per day. For example, if you shop for groceries once a week and go to some other stores daily, you might use about 4 bags per day.

another hint : You need to multiply your own use by 365 300 million.

I think I have the answer: your daily use one hundred billion

In fact, according to reusablebags.com, the number is about 4.6 10 11, or 460 billion.

Notice that I am being a little cavalier with the numbers here. I say I use about 4 bags a day, and multiply by about one hundred million. Not only is it OK to be a little vague, its absolutely necessary, otherwise you re claiming more knowledge than you actually have. Saying:

Americans use about 4.6 hundred billion bags/yr

is a reasonable statement. But saying

Americans use 304,339,593 365 4 444,335,805,780 bags/yr

is ridiculous, and it makes you sound like a pompous know-it-all to boot. For one thing, the U.S. population has changed since I wrote the above equation. For another thing, 4 bags a day was only a rough guess. And technically years have 365.25 days.

So I really don t know how many bags were used, but if I did enough research, I hope to be able to say between 4 and 5 hundred billion, or even in the hundred-billion range. In other words, not trillions, not millions, but hundreds of billions.

The next problem is easy, but don t skip it:

M M s

How many m m s are there in a one-pound bag, if a bag weighing 1/11 of a pound has 35 m m s.

I need a hint : 11 of the little bags would go into one big bag

I think I have the answer: about 35 11 about 400 m ms.

Yes, I know 35 11 is 385, but do you really want to claim that a pound of m m s contain exactly 385 pieces. Based on me eating -- I mean, counting -- a single fun-size pack.

Also, notice in this problem I didn t tell you how much the small bag weighed, only that it contained 1/11 of the amount of a large bag. Still, you probably found it easy to determine that you needed to multiply by 11. This is called multiplying by the reciprocal.

Reciprocal, in this case, means what you get when you flip a fraction upside down. It s the over part of one over eleven.

And yes, this is a biology class :

Bacterial contamination:

Some students are measuring bacterial contamination. They take a very small sample of the contaminated food -- about one-ten-thousandth 1/10,000 of the container -- and count 49 bacterial cells. How many bacteria were in the original container of food.

I need a hint : The students took a 1/10,000 sample, so what do they need to multiply by.

another hint : Multiply the number found by the reciprocal of 1/10,000

I think I have the answer: about 490,000.

Again, when we say about 490,000, we really mean more than 485,000 but less than 495,000. There are statistical ways to determine exactly what range you think the anwer lies in, but we ll save that for a different module.

If you found this last problem easy, that s great. Multiplying by the reciprocal of your sample size is the heart of counting bacteria by the serial diluation method. The rest is just technique.

Speaking of technique just how did those students get a sample of 1 ten-thousandth of the bacteria in their food. I know kids have a hard time just dividing a cookie into 3 equal pieces. Well, that s where the technique comes in. Basically, it s awfully hard to divide something into teeny-tiny pieces unless you first blow that something up and make it huge. That s what the story on the next page is about

The queen who made the stock

Once Upon a Time, there was an unbearably snobby queen-mother with a son of marriageable age. The son was smart, charming, and funny, but not one of the princesses that he brought home was good enough for his mother. One day, while daydreaming in his calculus lecture, the prince met his true love. He was giddy with emotion, but realized that convincing his mother would take some work.

The prince looks giddy

When the prince and his intended arrived at the palace for spring break, he found his mother uncharacteristically in the kitchen. I ve made your favorite, cooed his mother unconvincingly, split pea soup. My very own recipe. 9 million very small peas per liter. I m sure your little friend will love it. But if not, well, not everyone is made for royalty.

The prince looked at the mushy glutinous mass in his mother s cauldron with dismay. He knew that his relationship was doomed if he didn t find a way out. He racked his brain for solutions, but his courseload of calculus, microbiology, organic chemistry, and analysis of Swiss yodeling had left little room for culinary improvement. In other words, he could barely boil an egg. Frantically he considered derivatives, limit theorems, integrals and natural logarithms, but they all seemed a bit, well, complicated, given that dinner was to be served in six minutes and his mother was out adding a fifth spoon to every place setting.

The prince s sister dilutes the soup

Just then his younger sister entered the kitchen and saw his miserable face. When he explained the predicament, she just smiled and said all you need is plain old multiplication. In vain the prince tried to explain that he needed to dilute the soup, not multiply it. Exactly. said his sister. Anyone can eat a soup that has 90 peas per liter. All we have to do is figure out how to get it diluted to that level. So

That s a dilution factor of 100 to 1. That way, each liter of soup will have only 90,000 peas instead of 9 million.

Yeah, but we ll also have 100 liters of soup. There s not enough tupperware here for all that food.

OK, that s a good point. I didn t think of that Well, we don t need to mix up all 100 liters. All Mumsy expects is a single pot. And all that matters is that we get the ratio right hmm let s say we started with a hundredth of a pot of the old soup and added 99 hundredths of a pot of water.

What do we do with the rest of the soup.

Um, keep it for your next girlfriend.

Luckily, the kingdom measured in metric only. One soup pot held 1 liter of soup, so the sister removed 10 mLs and put it into a clean pot. She then filled the pot to the brim with water. Voila, soup with only 90,000 peas per liter.

The prince gave it a try and promptly spit it back out again. Blaaah, still too much. Its nasty he said, just as his second sister came in. A quick conference between sisters brought the second sister up to speed. Let s do the same thing again. said the second sister enthusiastically.

Great, it didn t work the first time, so now we re going to do it again.

Yes, we already got it partway diluted, now we ll just dilute it some more.

So Sister 2 took 10 mL of the diluted soup, put it in a third pot, and filled that pot to the brim with water.

The prince gave the double-diluted soup a try. Still too strong, he muttered. Cue Sister 3, another explanation of soup, mothers, and true love, and you should be able to see it coming a third dilution. But this time, going from 900 to 90 peas per liter required only a ten to 1 dilution. Hence the third sister put 100 mLs of soup one tenth of the total into a new pot, and filled the pot full to the liter mark:

The princess drinks the thrice-diluted soup.

The prince tried the triple-diluted soup. Wow. Fantastic. It tastes just like water.

At dinner the prince s girlfriend slurped down the watery soup like a trooper.

Sadly, the prince s mother was not blind or totally stupid. She quickly caught on to the soup-dilution scheme, found the leftover stock, dumped it over the prince s head, and sent the girlfriend packing. The prince passed calculus, graduated with slight honors, and lived out his life in bitter isolation. Moral of the story: don t mess with mumsy.

OK, there might be a few other morals:

Serial dilution means you do a series of dilutions, where each dilution gets you closer to your goal.

Each dilution can be seen as a conversion of a concentrated stock into a diluted stock. This is pretty obvious when you re dealing with factors of 10 or 100, but could be trickier if you had to use less comfortable numbers.

It doesn t really matter how much stock you start with, the important thing is to take out the right fraction of it a tenth, a hundredth and then add enough water to get back to the initial volume.

Oct 19, 2009 Fifth video in a series of videos discussing concentration calculations commonly used in a laboratory. More specifically a molecular biology lab. This.
Calculate serial equation with simple serial dilution calculator. Simply provide concentration and dilution values to get serial dilution calculation.
Serial Dilution: How it works. The story on the previous pages has many parallels with life in a microbiology lab. Frequently, you will find it necessary to add.

When you re thinking about dilution, it helps to simplify your actions into dilution factors. When we said the diluted coffee was

1/10th as strong as the original

that was a dilution factor. We could also have said

the dilution factor was 1/10, or

the dilution factor was 0.1.

Here are a few more for you to try:

1 mL coffee 4 mL water

1 mL coffee 9mL water

1 mL 99mL water

As you ve probably guessed, this works exactly the same whether you re talking about caffeine or meningicocci. Here s what a dilution factor of 0.01 looks like on the lab bench:

Notice that it really doesn t matter how much of the original stock you started with, as long as you had enough to put 1 mL into the new container. What matters is how much you transfer and how much water you add.

It s possible to write an algebraic expression for the dilution factor, but it s almost more trouble than it s worth, because it sounds so complex. But for what it s worth, the dilution factor for 1 mL stock 99 mL water is:

amount transferred / total amount

amount transferred / amount transferred amount water added

1 / 1 99 1/100 0.01.

Below is an applet to practice finding dilution factors, and also to determine how much water to add to achieve a given dilution. You should practice this until it is second nature..

1 mL stock mL water

Can you do it in your sleep. OK, then go on to the next page

Now that you are very comfortable with dilution factors what happens if you dilute and then dilute again. For example, we could take super-strong cofee, dilute it by 1/5, then dilute THAT by 1/10. So,

Here s the rule:

To find the overall or total dilution factor,

simply multiply the dilution factors for each step.

Once again, here s an applet to practice finding the total dilution scheme, regardless of how the dilution scheme is expressed -- as directions, as fractions, or as decimals.

Remember, keep going until you re very comfortable with the calculations Oh, and do yourself a favor, use a calculator..

Given the following series of dilutions,

what is the total dilution factor.

As a Fraction: 1 /

As a Decimal:

feedback here

So let s put some of these skills together to design dilution schemes -- you don t want to be a lab grunt all your life, right.

So to do this, you need to figure out the overall dilution you re shooting for. In this case, just take the concentration you want to achieve, and divide it by the concentration you currently have. As an example, if you want coffee with 5 caffeine molecules per mL, but the coffee you have has 5000, you need a dilution of 5/5000, or 0.001.

The trickier part is figuring out a series of dilutions that will achieve your overall dilution. In these examples, the numbers will always come out evenly if you choose dilutions of 1/2, 1/5, 1/10, or their multiples. Use the scratchpad to check your plans, and if you get completely lost, click the. button for a workable dilution scheme.

You might not be able to do this in your sleep, but at least work at it until it makes sense

Design some dilutions

You have a stock with an estimated 40,000 CFUs per mL, and you need to dilute to an estimated 500 CFUs per mL.

What overall dilution factor do you need.

How could you achieve this total dilution in three steps.

1 mL --

mL water, then

1 mL --

mL water.

scratchpad

test your dilution factors here :

So far we ve figured out how to make a dilution, which we can then plate and count. But by definition, we re counting only a fraction of what was originally there. How do we account for that. By scaling up.

Scaling up means starting from a sample and figuring out how many were in the original brew, or stock, or whatever was originally there.

For example, we can start with a cup of wimpy coffee and figure out how much caffeine was in the original brew. All we need to know is what the overall dilution factor was. In the case of wimpy coffee, it was 1/50, or 0.02.

So, when we count the caffeine molecules in a cup of wimpy coffee, we know we got 1/50th of what was in a cup of the original brew -- or in other words, there was 50 times as much in a cup of the original. This method is called multiplying by the inverse of the dilution factor.

If the dilution factor is in the form of a fraction,

flip the fraction

i.e., 1/50 becomes multiply by 50/1.

If the dilution factor is in decimal form,

multiply by 1 over the decimal

i.e., 0.02 becomes multiply by 1/0.02.

Finally, notice that I m telling you the total number of caffeine molecules ONE CUP of the original brew. If I don t know the actual amount of original brew, I also won t know how much caffeine there was total.

Back to the lab

Here are some problems, ranging from easy to a bit hard

I did a series of dilutions with an overall dilution factor of 1/20,000, and then plated a grew a 1mL sample. After 1 day, I counted 27 CFUs on the petri dish. How many CFUs would there be per 1mL of the original stock.

To make this problem interactive, turn on javascript.

I need a hint :

inverse of 1/20,000 is 20,000

another hint :

27 20,000

I think I have the answer:540,000 per mL

I did a series of dilutions, with dilution factors of 0.1, 0.1, and 0.01. At the end I plated and grew a 1mL sample, and counted 48 CFUs. How many CFUs would there be per 1mL of the original stock.

What s the overall dilution factor.

overall dilution factor 0.1 0.1 0.01 0.0001

Multiply by the inverse

I think I have the answer: 48 1/0.0001 480,000 CFUs per mL

I did a series of dilutions as follows:

1 mL added to 9 mLs water

1 mL added to 99 mLs water

1 mL added to 49 mLs water

If the final 1mL sample had 152 colonies, what was the original concentration.

The dilution factors were 1/10, 1/100, and 1/50

The overall dilution was 1/50,000

I think I have the answer:152 50,000 7,600,000 cells/mL

Once again, let s take a breather from the theory and practice. This is one of the do-it-in-your-sleep kind, and it has two steps:

Look at the dilution scheme to determine the total dilution factor

Look at the plate and scale up to determine the total CFUs per mL.

Scaling up

question

Total dilution factor decimal

to total number

Your browser does not support html canvas. There were CFUs on the plate.

How many CFUs would there be

in 1mL of the original stock.

Remember the picture of the hell-to-count petri dish with 500 colonies. No one wants that to happen to them, especially late on a Friday afternoon. But on the other hand, how can we avoid it.

Very easily while we re doing our dilutions, we just keep plating each intermediate step. Then the next day, we decide which plate looks like the most reasonable for counting. Since we cleverly labeled each plate with its overall dilution factor, we also know how to scale back up to get the original concentration.

So, now we finally have all the pieces of serial dilution assembled:

Dilute

Calculate dilution factor

Plate

Repeat

To make things easier, the standard operating procedure is to go by factors of 10, and to do about 5 or 6 plates altogether.

Content on this page requires a newer version of Adobe Flash Player.

Let s say I guesstimate that I have about 42 million CFUs per mL -- I might want to start with a first dilution of about 1/1000, and plate that. Then I make 4 more 1/10 dilutions, plating each one in turn. In the end, I have 5 plates, labeled as shown below. And, if you roll over the image, you will see the plate counts I expect if my original guess 42 million was approximately correct. Oh, and TMTC means Too Many To Count.

For this, we have any easy rule of thumb: the plate you count should have between 30 and 300 colonies. Use your mouse below to see how this works.

This rule of thumb has the undeniable advantage of being easy to use. But why does it work.

Let s imagine that we have a sample with exactly 42 million cells per mL. And let s say that our technique is flawless. If we count a 1:1,000,000 diluted plate, we should find exactly 42 CFUs remember, we have magically flawless technique. But the exact same thing would happen if our sample started with 42,000,001 cells. Or 42,001,000 cells. Or even 42,100,000 cells. In fact, even with our absolutely flawless technique, the best we can say is that there are between 41,500,000 and 42,500,000 cells. So our absolutely unavoidable error is plus or minus 500K/42million -- about 1.1. That s pretty good.

Let s look at some other ways we could count the same 42 million cell sample:

Dilution Factor

plate count

resolution

ease of counting

,000

4200

41,005,000 to 41,005,000

/- 5000 0.011

great..

NOPE, can t do it, this is too much to count

0,000

420

41,050,000 to 41,050,000

/- 50,000 0.11

still great

SORRY, still too hard to count

1:1,000,000

41,500,000 to 41,500,000

/- 500,000 1.1

not too bad

easy to count

,000,000

35,000,000 to 45,000,000

/- 5 million 11

ACK. mayday.

chimpanzees can count this plate.

The more we dilute, the easier the counting, but the higher the error. So you can see that the 30 to 300 guideline is really a compromise between countability and error.

Here is a chance for you to put all of the steps together, using viable plate count and serial dilution to quantify a bacterial population

Here is some practice with different dilution schemes. This time the applet will do the counting for you. The first problem should be very easy at this point, but after that you can click on Hard Problem to get trickier dilution schemes.

Below are a few unusual situations things do go wrong, of course, and you should be able to recognize that. If you think the dilution series is not valid, click on re-do the dilution.

dilution factor

0,000

1:1,000,000

,000,000

0,000,000

count

TMTC

674

answer

375

105

,000

249

954

567

Remember Frank. He s still sitting on the examining table with a coat over his head. In fact about 50 of people with meningitis will die when the bacterial levels in their blood stream reach 500 / mL.

The worried nurse hands you a vial of 10 mLs of Frank s blood. How can you decide whether the infection is at a lethal level.

What counting method will you use.

Unfortunately, a direct count or a photospec would require separating the meningicocci from the red blood cells. If we could do that, we could probably just cure poor Frank. So we re stuck with a viable plate count.

What dilution scheme will you use.

We need to get plate counts between 30 and 300, and we think that the concentration in his blood might be as high as 500 per mL, but it could be much lower. So, we should go ahead do the first plate without even diluting. After that we could do standard 1/10th dilutions.

How many dilutions do you need.

You definitely need at least 1 dilution, in case Frank is somewhere in the 300 or 400 per mL range. Without a dilution, that wouldn t be countable.

But really, a single 1/10th dilution would suffice. If Frank has 300 colonies in a 1/10th dilution, he has 3000 actual cells per mL, and that would be fatal. Of course, he d also be dead, but let s not be morbid.

However, you could keep going with a standard 5 dilutions and not waste much time or energy, plus it would allow you to make an accurate estimate regardless of his actual level of meningicocci in the blood.

Make sure you understand the following concepts -- go back to the applets if you need to:

dilution factor stated as a fraction or decimal

overall dilution factor product of individual dilution factors

choosing the plate to count 30 to 300 CFUs

scaling up from the plate to the population size multiplying by the inverse

setting up an appropriate dilution scheme to result in a countable plate

Let s say a culture contains about a million CFUs. At 1 CFU per second, that would take 11.6 days to count. Assuming you didn t stop to eat or sleep.

Clearly a better way is needed.

And clearly, this module is going to pick that method apart and pound it into the figurative whiteboard.

So let s get started already.

First of all, we re going to use the Viable Plate Count method -- the only method that can tell a live cell from a dead one for a rundown on counting methods, look here. So, we re going to take a little bit of our culture, put it on a plate, and grow it up. But we still have a problem -- too many colonies to count. For example, even 500 colonies on a petri dish would look something like this:

What if you are trying to count a population in the thousands or millions. You could literally have a carpet of colonies also known as a confluent lawn growing on your petri dish. This is where dilution saves the day. Not just dilution, but serial dilution meaning dilution over and over again.

Why do we dilute. To have less to count

Why do we do it repeatedly. Because we don t know how much dilution we need. Every time we dilute, we ll also make a new plate to incubate. So we might do 5 dilutions and grow up 5 plates. Then we ll end up throwing away 4 of them. Sound wasteful. Well, dilution and plating is quick and easy compared to the pain of starting your experiment all over again.

Of course, lots of things can be diluted, not just blood samples

So let s see what the process of diluting looks like.

Here s an everyday example:

Cold Press coffee is a superstrong form coffee that starts out with about a zillion molecules of caffeine per cup. In order to actually be able to drink the stuff, you have to dilute it.

For example, you could put one cup of cold press coffee into a pot and add 9 cups of water.

How many molecules of caffeine are in the pot.

How many cups of coffee are in the pot.

If you pour 1 cup from the pot, how many molecules of caffeine will it have.

Let s look at this in graphical form:

Simple, right. Of course, we don t want to have to draw pictures every time we do a dilution, so we could simply write:

1 cup coffee 9 cups water -- 1/10th as strong as the original.

The MicrobeLibrary includes peer-reviewed visual resources and laboratory protocols for undergraduate microbiology and science education supported by the American.